Tucker circles
The Tucker circles are a generalization of the cosine circle and first Lemoine circle.
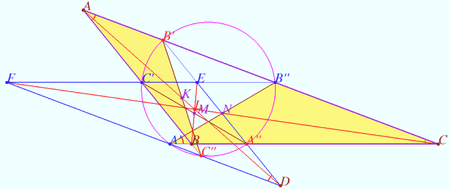
Tucker circle
Let triangle ![]() be given.
be given. ![]() is it’s circumcenter,
is it’s circumcenter, ![]() is it’s Lemoine point.
is it’s Lemoine point.
Let homothety centered at ![]() with factor
with factor ![]() maps
maps ![]() into
into ![]() .
.
Denote the crosspoints of sidelines these triangles as
![]()
![]()
Prove that points ![]() and
and ![]() lies on the circle centered at
lies on the circle centered at ![]() (Tucker circle).
(Tucker circle).
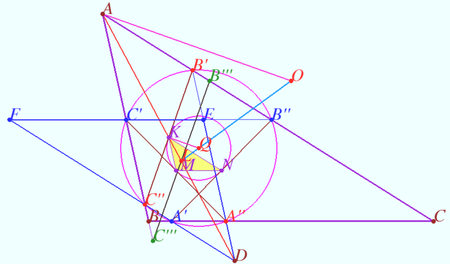
Proof
![]() is the parallelogram.
is the parallelogram.
Denote ![]()
![]() is antiparallel to
is antiparallel to ![]()
Similarly, ![]() is antiparallel to
is antiparallel to ![]() is antiparallel to
is antiparallel to ![]()
![]() is midpoint
is midpoint ![]() is the midpoint
is the midpoint ![]()
![]()
![]()
Similarly, ![]()
Let ![]() be the symmedian
be the symmedian ![]() through
through ![]()
![]()
It is known that three symmedians through ![]() are equal, so
are equal, so ![]()
![]() is homothetic to
is homothetic to ![]() with center
with center ![]() and factor
and factor ![]()
So segments ![]() are tangents to
are tangents to ![]() and points of contact are the midpoints of these segments.
and points of contact are the midpoints of these segments.
Denote ![]() the circumcenter of
the circumcenter of ![]()
Therefore ![]()
vladimir.shelomovskii@gmail.com, vvsss
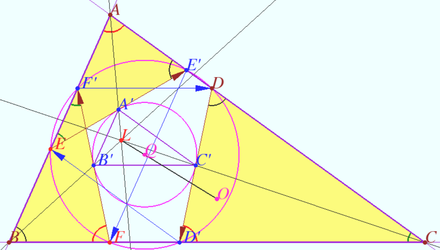
Tucker circle 2
Let triangle ![]() be given. Let
be given. Let ![]() be the arbitrary point on sideline
be the arbitrary point on sideline ![]()
Let ![]() be the antiparallel to side
be the antiparallel to side ![]()
Denote point ![]()
Let ![]() be the antiparallel to side
be the antiparallel to side ![]()
Denote point ![]()
Let ![]() be the antiparallel to side
be the antiparallel to side ![]()
Prove that points ![]() and
and ![]() lies on the circle centered at
lies on the circle centered at ![]() (Tucker circle).
(Tucker circle).
Proof
![]() is isosceles trapezoid.
is isosceles trapezoid.
So ![]()
![]() is isosceles trapezoid.
is isosceles trapezoid.
So ![]()
Denote ![]() the midpoint
the midpoint ![]() the midpoint
the midpoint ![]() the midpoint
the midpoint ![]()
![]() Similarly,
Similarly, ![]()
![]() is the midpoint of antiparallel of
is the midpoint of antiparallel of ![]() is the
is the ![]() symmedian of
symmedian of ![]()
Similarly, ![]() is the
is the ![]() symmedian,
symmedian, ![]() is the
is the ![]() symmedian of
symmedian of ![]()
Therefore Lemoine point ![]() is homothetic to
is homothetic to ![]() with center
with center ![]()
So segments ![]() are tangents to
are tangents to ![]() and points of contact are the midpoints of these segments.
and points of contact are the midpoints of these segments.
Denote ![]() the circumcenter of
the circumcenter of ![]() where
where ![]() is the circumcenter of
is the circumcenter of ![]()
Therefore ![]()
vladimir.shelomovskii@gmail.com, vvsss