Difference between revisions of "1983 AHSME Problems/Problem 17"
Sevenoptimus (talk | contribs) m (Improved grammar) |
Pinotation (talk | contribs) (→Solution 1 (Linear Modeling)) |
||
| (5 intermediate revisions by 2 users not shown) | |||
| Line 12: | Line 12: | ||
\textbf{(E)} \ E </math> | \textbf{(E)} \ E </math> | ||
| − | ==Solution== | + | ==Solution 1 (Linear Modeling)== |
| + | |||
| + | The reciprocal of a number \( a \) is \( \frac{1}{a} \). | ||
| + | |||
| + | We start with \( F \) and the point \( (1, 0i) \) where \( i = \sqrt{-1} \). Draw a line through these two points. | ||
| + | |||
| + | The reciprocal of a line is legitimately a vertical shrink or a horizontal stretch (the line gets farther away from the \( i_1 \) axis but closer to the real axis). Therefore the line must pass through point <math>\boxed{\textbf{C}}</math> as it is the only point that is closest to the real axis whilst maintaining a reflection over the imaginary axis. | ||
| + | |||
| + | ~Pinotation | ||
| + | |||
| + | ==Solution 2== | ||
Write <math>F</math> as <math>a + bi</math>, where we see from the diagram that <math>a, b > 0</math> and <math>a^2+b^2>1</math> (as <math>F</math> is outside the unit circle). We have <math>\frac{1}{a+bi} = \frac{a-bi}{a^2+b^2} = \frac{a}{a^2+b^2} - \frac{b}{a^2+b^2}i</math>, so, since <math>a, b > 0</math>, the reciprocal of <math>F</math> has a positive real part and negative imaginary part. Also, the reciprocal has magnitude equal to the reciprocal of <math>F</math>'s magnitude (since <math>|a||b| = |ab|</math>); as <math>F</math>'s magnitude is greater than <math>1</math>, its reciprocal's magnitude will thus be between <math>0</math> and <math>1</math>, so its reciprocal will be inside the unit circle. Therefore, the only point shown which could be the reciprocal of <math>F</math> is point <math>\boxed{\textbf{C}}</math>. | Write <math>F</math> as <math>a + bi</math>, where we see from the diagram that <math>a, b > 0</math> and <math>a^2+b^2>1</math> (as <math>F</math> is outside the unit circle). We have <math>\frac{1}{a+bi} = \frac{a-bi}{a^2+b^2} = \frac{a}{a^2+b^2} - \frac{b}{a^2+b^2}i</math>, so, since <math>a, b > 0</math>, the reciprocal of <math>F</math> has a positive real part and negative imaginary part. Also, the reciprocal has magnitude equal to the reciprocal of <math>F</math>'s magnitude (since <math>|a||b| = |ab|</math>); as <math>F</math>'s magnitude is greater than <math>1</math>, its reciprocal's magnitude will thus be between <math>0</math> and <math>1</math>, so its reciprocal will be inside the unit circle. Therefore, the only point shown which could be the reciprocal of <math>F</math> is point <math>\boxed{\textbf{C}}</math>. | ||
| + | |||
| + | ==Solution 3 (Polar Form)== | ||
| + | |||
| + | Let <math>z = r(\cos\theta + i\sin\theta)</math> be the complex number at <math>F</math> in polar form. Then <math>\frac{1}{z} = \frac{1}{r}(\cos(-\theta) + i\sin(-\theta))</math>. Since <math>F</math> is outside the circle, <math>r > 1</math>, and therefore <math>\frac{1}{r} < 1</math>. So <math>\frac{1}{z}</math> must be inside the circle and on the line which is <math>\theta</math> clockwise from the real axis, that is <math>\boxed{(\mathbf{C})\ C}</math>. | ||
| + | |||
| + | -j314andrews | ||
==See Also== | ==See Also== | ||
Latest revision as of 01:18, 25 September 2025
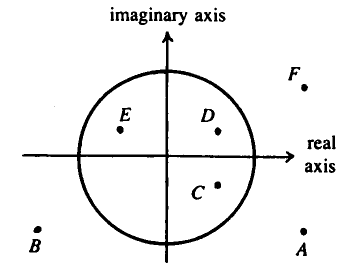
Problem
The diagram above shows several numbers in the complex plane. The circle is the unit circle centered at the origin.
One of these numbers is the reciprocal of ![]() . Which one?
. Which one?
![]()
Solution 1 (Linear Modeling)
The reciprocal of a number \( a \) is \( \frac{1}{a} \).
We start with \( F \) and the point \( (1, 0i) \) where \( i = \sqrt{-1} \). Draw a line through these two points.
The reciprocal of a line is legitimately a vertical shrink or a horizontal stretch (the line gets farther away from the \( i_1 \) axis but closer to the real axis). Therefore the line must pass through point ![]() as it is the only point that is closest to the real axis whilst maintaining a reflection over the imaginary axis.
as it is the only point that is closest to the real axis whilst maintaining a reflection over the imaginary axis.
~Pinotation
Solution 2
Write ![]() as
as ![]() , where we see from the diagram that
, where we see from the diagram that ![]() and
and ![]() (as
(as ![]() is outside the unit circle). We have
is outside the unit circle). We have ![]() , so, since
, so, since ![]() , the reciprocal of
, the reciprocal of ![]() has a positive real part and negative imaginary part. Also, the reciprocal has magnitude equal to the reciprocal of
has a positive real part and negative imaginary part. Also, the reciprocal has magnitude equal to the reciprocal of ![]() 's magnitude (since
's magnitude (since ![]() ); as
); as ![]() 's magnitude is greater than
's magnitude is greater than ![]() , its reciprocal's magnitude will thus be between
, its reciprocal's magnitude will thus be between ![]() and
and ![]() , so its reciprocal will be inside the unit circle. Therefore, the only point shown which could be the reciprocal of
, so its reciprocal will be inside the unit circle. Therefore, the only point shown which could be the reciprocal of ![]() is point
is point ![]() .
.
Solution 3 (Polar Form)
Let ![]() be the complex number at
be the complex number at ![]() in polar form. Then
in polar form. Then ![]() . Since
. Since ![]() is outside the circle,
is outside the circle, ![]() , and therefore
, and therefore ![]() . So
. So ![]() must be inside the circle and on the line which is
must be inside the circle and on the line which is ![]() clockwise from the real axis, that is
clockwise from the real axis, that is ![]() .
.
-j314andrews
See Also
| 1983 AHSME (Problems • Answer Key • Resources) | ||
| Preceded by Problem 16 |
Followed by Problem 18 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 • 26 • 27 • 28 • 29 • 30 | ||
| All AHSME Problems and Solutions | ||
These problems are copyrighted © by the Mathematical Association of America, as part of the American Mathematics Competitions. ![]()